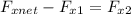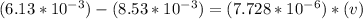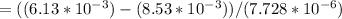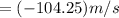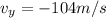Question

A 6.72 particle moves through a region of space where an electric field of magnitude 1270 N/C points in the positive direction, and a magnetic field of magnitude 1.15 T points in the positive direction. If the net force acting on the particle is 6.13E-3 N in the positive direction, calculate the magnitude of the particle's velocity. Assume the particle's velocity is in the - plane.

Answer 1

`v_(y) = -104 m/s`

Step-by-step explanation:

Using:

Force = electric field * charge

`F=e*q`

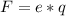
Force = magnitude of charge * velocity * magnetic field * sin tither

`F_(x2)= |q|*v*B*sin \alpha`

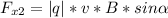
Force on particle due to electric field:

`F_(x1)= E*q = (1270N/C)*(-6.72*10^(-6) ) = -8.53*10^(-3)`

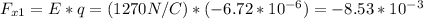
Force on particle due to magnetic field:

`F_(x2)= |q|*v*B*sin \alpha = (6.72*10^(-6) )*(1.15)*(sin90)*v = (7.728*10^(-6))*(v)`

`F_(x2)` is in the positive x direction as
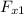`F_(x1)` is in the negative x direction while net force is in the positive x direction.

Magnetic field is in the positive Z direction, net force is in the positive x direction.

According to right hand rule, Force acting on particle is perpendicular to the direction of magnetic field and velocity of particle. This would mean the force is along the y-axis. As this is a negatively charged particle, the direction of the velocity of the particle is reversed. Therefore velocity of particle, v, has to be in the negative y direction.

Now,

`F_(xnet)- F_(x1 ) = F_(x2 )`

`(6.13*10^(-3)) - (8.53*10^(-3) ) = (7.728*10^(-6))*(v)`

`v = (F_(xnet) - F_(x1)) / (F_(x2) )`

`=((6.13*10^(-3) ) - (8.53*10^(-3))) / (7.728*10^(-6))`

`= (- 104.25) m/s`

`v_(y) = -104 m/s`