Question

In an experiment, a variable, position-dependent force F(x) is exerted on a block of mass 1.0kg that is moving on a horizontal surface. The frictional force between the block and the surface has a constant magnitude of Ff . In addition to the final velocity of the block, which of the following information would students need to test the hypothesis that the work done by the net force on the block is equal to the change in kinetic energy of the block as the block moves from x=0 to x=5m ?

(A) The function F(x) for 0 < x < 5 and the value of Ff.
(B) The function a(t) for the time interval of travel and the value of Ff.
(C) The function F(x) for 0 < x < 5, the block's initial velocity, and the value of Ff.
(D) The function a(t) for the time interval of travel, the time it takes the block to move 5 m, and the value of Ff.
(E) The block's initial velocity, the time it takes the block to move 5 m, and the value of Ff.

Answer 1

(C) The function F(x) for 0<x<5, the block's initial velocity, and the value of Ff

Step-by-step explanation:

From physics, we know that the work done by a force is given by the following integral:

`Work=\int\limits^(x_f)_(x_0) {F(x)} \, dx`

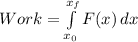
Where F(x) is the net force function.

The net force is given by the sum of forces:

`\Sigma F=ma`

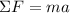
In this case there are only two forces we care about, F(x) and Ff, so the sum of forces will be:

`F(x)-Ff=ma`

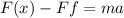
In this case Ff is negative because it acts against the force F(x)

So our integral will now look like this:

`\int\limits^(x_f)_(x_0) {F(x)-Ff} \, dx = \int\limits^(x_f)_(x_0) {ma} \, dx`

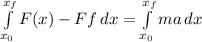
Now, we also know that the acceleration is defined to be:

`a=(dv)/(dt)`

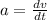
so we can do the substitution:

`\int\limits^(x_f)_(x_0) {F(x)-Ff} \, dx = \int\limits^(x_f)_(x_0) {m(dv)/(dt)} \, dx`

we also know that:

`(dx)/(dt)=v`

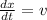
so we can substitute again and change the limits of integration of the right side of the equation, so we get:

`\int\limits^(x_f)_(x_0) {F(x)-Ff} \, dx = \int\limits^(v_f)_(v_0) {mv} \, dv`

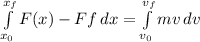
so when solving the integral we get:

`[F(x)-Ff](x_f-x_0)=(mv_(f)^(2))/(2)-(mv_(0)^(2))/(2)`

the right hand side of the equation:

`(mv_(f)^(2))/(2)-(mv_(0)^(2))/(2)`

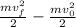
will be the difference of kinetic energy which proves the hypothesis.

In this case, we know what the mass is, and the x-values. So besides the final velocity, we need to know the initial velocity, the force F(x) for 0<x<5 and the friction Ff, so the answer will be (C)

Answer 2

Answer: correct option is C

The function F(x) for 0 < x < 5, the block's initial velocity, and the value of Ff.

Explanation:

The total work done = P.E + K.E

K.E = 1/2mv^2

The speed V depends on the position:

0 < x < 5

Also, since work done = F × distance x

The workdone also depends on F(x)

The net force = 0 that is

F + fr = 0

Where fr = frictional force.

Therefore the best option for the hypothesis of work done will be;

The function F(x) for 0 < x < 5, the block's initial velocity, and the value of Ff.