Question

Advandia is a drug used to treat diabetes, but it may cause an increase in heart attacks among a population already susceptible. A large study found that out of 1,456 diabetics who were treated with Avandia, 27 of them had a heart attack during the study period. This was compared with 41 heart attacks among a group of 2,895 participants who were given other treatments for their diabetes. The researchers want to determine if there is evidence to suggest that there is a significant increase in the proportion of people who suffer heart attacks when using Avandia compared to other treatments.

a)Are these proportions from matched-pairs data?

b)What is the result of the appropriate hypothesis test, using ? = 0.05 level of significance?

Answer 1

Answer:(a)No, it is not a matched pair data

(b) we accept the null hypothesis

Explanation:

(a) No, it is not a matched pair data

(b) Given that x₁ = 27, x₂ = 41, n₁= 1456, n₂ = 2895

P₁= x₁/n₁ = 27/1456 = 0.0185, P₂ = x₂/ n₂ = 41/2895 = 0.0142

Step 1 The Null hypothesis H₀ ; p₁≤ p₂

The Alternate Hypothesis ; H₁ ; p₁ >p₂

The level of significance α = 0.05

Step 2 The test significance z = p₁ - p₂

√pq (1/n₁ +1/n₂)

where p= n₁p₁ + n₂p₂ = 27+ 41

n₁+n₂ 1456+ 2895 = 0.0156

q = 1- 0.0156 = 0.9844

z= 0.0185 - 0.0142

√(0.0156)(0.9844) (1/1456 + 1/2895)

= 0.0043/0.004 = 1.075

Zcal = 1.075

Step 3 Criterion ; if Zcal < Ztab, Accept Null hypothesis

otherwise reject Null hypothesis

Ztab at 0.05 LOS is 1.645 = zα/2

Stepn 4; Conclusion Since Ztab = 1.075 < 1.645 = Zcal

We accept the Null hypothesis which means there is no evidence to increase the first proportion

Step 5: p- value; F(1.645) -F91.075) = 0.9495 - 0.0918> 0.05

Therefore we accept the null hypothesis

Answer 2

a) The proportions are not form matched-pairs data.

b) The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that there is evidence of a significant increase in the proportion of people who suffer heart attacks when using Avandia compared to other treatments.

Explanation:

a) Two data sets are "paired" when the following one-to-one relationship exists between values in the two data sets:

• Each data set has the same number of data points.

• Each data point in one data set is related to one, and only one, data point in the other data set.

None of this conditions apply in this case, so the proportions are not form matched-pairs data.

b) This is a hypothesis test for the difference between proportions.

The claim is that there is evidence to suggest that there is a significant increase in the proportion of people who suffer heart attacks when using Avandia compared to other treatments.

Then, the null and alternative hypothesis are:

`H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2> 0`

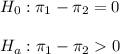
The significance level is 0.05.

The sample 1 (Avindia treatment), of size n1=1456 has a proportion of p1=0.0185.

`p_1=X_1/n_1=27/1456=0.0185`

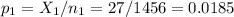
The sample 2 (other treatment), of size n2=2895 has a proportion of p2=0.0142.

`p_2=X_2/n_2=41/2895=0.0142`

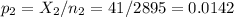
The difference between proportions is (p1-p2)=0.0044.

`p_d=p_1-p_2=0.0185-0.0142=0.0044`

The pooled proportion, needed to calculate the standard error, is:

`p=(X_1+X_2)/(n_1+n_2)=(27+41)/(1456+2895)=(68)/(4351)=0.0156`

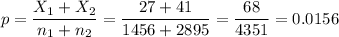
The estimated standard error of the difference between means is computed using the formula:

`s_(p1-p2)=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)}=\sqrt{(0.0156*0.9844)/(1456)+(0.0156*0.9844)/(2895)}\\\\\\s_(p1-p2)=√(0.00001+0.00001)=√(0.00002)=0.004`

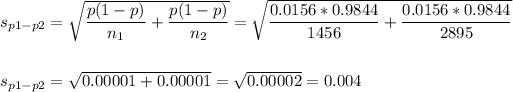
Then, we can calculate the z-statistic as:

`z=(p_d-(\pi_1-\pi_2))/(s_(p1-p2))=(0.0044-0)/(0.004)=(0.0044)/(0.004)=1.1`

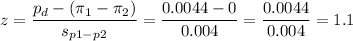
This test is a right-tailed test, so the P-value for this test is calculated as (using a z-table):

`P-value=P(z>1.1)=0.1358`

As the P-value (0.1358) is bigger than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that there is evidence to suggest that there is a significant increase in the proportion of people who suffer heart attacks when using Avandia compared to other treatments.