Question

A systems analyst tests a new algorithm designed to work faster than the currently-used algorithm. Each algorithm is applied to a group of 47 sample problems. The new algorithm completes the sample problems with a mean time of 20.29 hours. The current algorithm completes the sample problems with a mean time of 21.49 hours. The standard deviation is found to be 5.032 hours for the new algorithm, and 3.267 hours for the current algorithm. Conduct a hypothesis test at the 0.01 level of significance of the claim that the new algorithm has a lower mean completion time than the current algorithm. Let μ1 be the true mean completion time for the new algorithm and μ2 be the true mean completion time for the current algorithm. Step 3 of 4 : Determine the decision rule for rejecting the null hypothesis H0. Round the numerical portion of your answer to two decimal places.

Answer 1

Explanation:

Let μ1 be the true mean completion time for the new algorithm and μ2 be the true mean completion time for the current algorithm.

This is a test of 2 independent groups. The population standard deviations are not known. it is a one-tailed test.

Therefore, the population means would be μ1 and μ2.

The random variable is x1 - x2 = difference in the sample mean completion time of the new and current algorithms.

We would set up the hypothesis.

The null hypothesis is

H0 : μ1 ≤ μ2 H0 : μ1 - μ2 ≤ 0

The alternative hypothesis is

Ha : μ1 > μ2 Ha : μ1 - μ2 > 0

Since sample standard deviation is known, we would determine the test statistic by using the t test. The formula is

(x1 - x2)/√(s1²/n1 + s2²/n2)

From the information given,

x1 = 20.29

x2 = 21.49

s1 = 5.032

s2 = 3.267

n1 = 47

n2 = 47

t = (20.29 - 21.49)/√(20.29²/47 + 21.49²/47)

t = - 0.07

The formula for determining the degree of freedom is

df = [s1²/n1 + s2²/n2]²/(1/n1 - 1)(s1²/n1)² + (1/n2 - 1)(s2²/n2)²

df = [20.29²/47 + 21.49²/47]²/(1/47 - 1)(20.29²/47)² + (1/47 - 1)(21.49²/47)² = 345.41/3.7668

df = 92

We would determine the probability value from the t test calculator. It becomes

p value = 0.47

At a level of significance of 0.01, we would not reject the null hypothesis because the p value, 0.47 is > 0.01

Answer 2

- The decision rule, as we applied the P-value approach, is to reject the null hypothesis if the P-value is smaller than the significance level.

If the critical value approach was applied, the decision rule would have been reject the null hypothesis if the t-statistic is below t-critical=-2.37.

- The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the new algorithm has a lower mean completion time than the current algorithm (P-value=0.09).

Explanation:

This is a hypothesis test for the difference between populations means.

The claim is that the new algorithm has a lower mean completion time than the current algorithm.

Then, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2> 0`

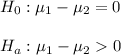
The significance level is 0.01.

The sample 1, of size n1=47 has a mean of 20.29 and a standard deviation of 5.032.

The sample 1, of size n1=47 has a mean of 21.49 and a standard deviation of 3.267.

The difference between sample means is Md=-1.2.

`M_d=M_1-M_2=20.29-21.49=-1.2`

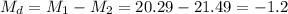
The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(5.032^2)/(47)+(3.267^2)/(47)}\\\\\\s_(M_d)=√(0.539+0.227)=√(0.766)=0.875`

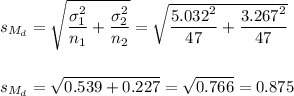
Then, we can calculate the t-statistic as:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(-1.2-0)/(0.875)=(-1.2)/(0.875)=-1.371`

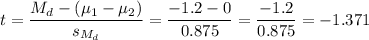
The degrees of freedom for this test are:

`df=n_1+n_2-1=47+47-2=92`

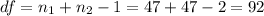
This test is a left-tailed test, with 92 degrees of freedom and t=-1.371, so the P-value for this test is calculated as (using a t-table):

`P-value=P(t<-1.371)=0.087`

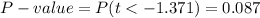
As the P-value (0.09) is bigger than the significance level (0.01), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the new algorithm has a lower mean completion time than the current algorithm.