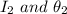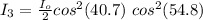Question

Unpolarized light is passed through polarizer 1. The light then goes though polarizer 2 with its plane of polarization at 40.7° to that of polarizer 1. Polarizer 3 is placed after polarizer 2. Polarizer 3 has its plane of polarization at 54.8° to the plane of polarization of polarizer 2 and at 95.5° to that of polarizer 1. What fraction of the intensity of the original light gets though the last polarizer?

Answer 1

The fraction of the intensity of the original light that got through the last polarizer is
`(I_3)/(I_o) = 0.0955`

Step-by-step explanation:

From the question we are told that

The angle between polarizer 2 and polarizer 1 is
`\theta_1 = 40.7^o`

The angle between polarizer 3 and polarizer 2 is
`\theta_ 2 = 54.8^o`

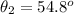
The angle between polarizer 3 and polarizer 1 is
`\theta _3 = 95.5^o`

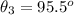
The intensity of light emerging from the first polarizer can be obtained using the one half rule as follows

`I_1 = (I_o)/(2)`

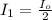
Here
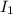`I_1` is the intensity of light emerging from the polarizer 1

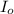`I_o` is the intensity of the unpolarized light

The intensity
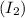`(I_2)`of light emerging from the second polarizer is obtained using the cosine-squared rule the intensity of light incidenting on the second polarizer is already polarized by the polarizer 1

So the intensity is mathematically represented as

`I_2 = I_1 cos^2 \theta_1`

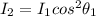
substituting for
`I_1`

`I_2 = (I_o)/(2) cos^2 \theta_1`

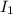
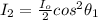
Substituting values

`I_2 = (I_0)/(2) cos^2 (40.7)`

The intensity
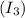`(I_3)` emerging from polarizer 3 is obtained using the cosine-squared rule as follows

`I_3 = I_2 cos^2 \theta_2`

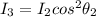
substituting for
`I_2 \ and \ \theta_2`

`I_3 = (I_o)/(2) cos^2 (40.7) \ cos^2 (54.8)`

`I_3 = (I_o)/(2) \ 0.5748 * 0.3323`

`I_3 =(0.0955) I_o`

`(I_3)/(I_o) = 0.0955`