Answer:
Expected cost = $6,750
Variance of the cost = $373,500
Explanation:
During normal 9 work hours: average number of calls = 7.0
Cost of each call = $50
During 15 off hours:
average number of calls = 4.0
Cost of each call = $60
Let's take U as the number of calls during the normal 9 hours.
I.e,

Therefore,
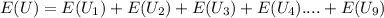
= 7+7+7+7+7+7+7+7+7
= 63
In Poisson random variable, Variance= mean, thus:
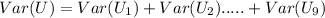
= 7+7+7+7+7+7+7+7+7
=63
Let's take V as the number of calls during the day's remaining 15 hours.
E(V) = Var(V)
= 15(4)
=60
The expected cost and the variance of cost associated with the calls received during a 24 hour day:
The expected cost =
$50U + $60V
= $50(63) + $60(60)
= $3150 + $3600
= $6750
The variance of the cost :
= Var(50U + 60V)
= 50²Var(U) + 60²Var(V)
= 2500*63 + 3600*60
= $373,500
Therefore, the expected cost is $6,750 and the variance of the cost is $373,500