Answer:
95% confidence interval for the percentage of all U.S. public high school students who are obese is [0.110 , 0.190].
Explanation:
We are given that 15% of a random sample of 300 U.S. public high school students were obese.
Firstly, the pivotal quantity for 95% confidence interval for the population proportion is given by;
P.Q. =
 ~ N(0,1)
~ N(0,1)
where,
 = sample % of U.S. public high school students who were obese = 15%
= sample % of U.S. public high school students who were obese = 15%
n = sample of U.S. public high school students = 300
p = population percentage of all U.S. public high school students
Here for constructing 95% confidence interval we have used One-sample z proportion statistics.
So, 95% confidence interval for the population proportion, p is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
 < 1.96) = 0.95
< 1.96) = 0.95
P(
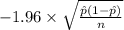 <
<
 <
<
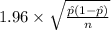 ) = 0.95
) = 0.95
P(
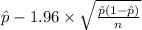 < p <
< p <
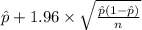 ) = 0.95
) = 0.95
95% confidence interval for p = [
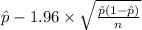 ,
,
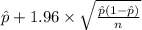 ]
]
= [
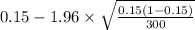 ,
,
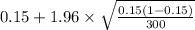 ]
]
= [0.110 , 0.190]
Therefore, 95% confidence interval for the percentage of all U.S. public high school students who are obese is [0.110 , 0.190].