Question

I'VE TRIED EVERY METHOD POSSIBLE TO ANSWER THESE QUESTIONS AND KEEP HITTING DEAD ENDS SO PLS IF YOU CAN HELP PLS DO BECAUSE I'M STUCK

A cone-shaped kitchen funnel has a diameter of 6 inches and a height of 7 inches. About how many times would you need to fill the funnel to fill a cylindrical can that has a radius of 4 inches and a height of 13 inches?

A. 3

B. 4

C. 9

D. 10

The circumference of an orange is approximately 37.68 centimeters. What is the approximate volume of the orange? Use 3.14 for π.

A. 226.08 cubic meters

B. 678.24 cubic meters

C. 904.32 cubic meters

D. 7234.56 cubic meters


Which of the following statements about the volume of a sphere and the volume of a cone are true? Select two answers.

A. You can find the volume of a sphere with only the diameter.

B. You can find the volume of a sphere with only the radius.

C. You can find the volume of a cone with only the height.

D. You can find the volume of a cone with only the diameter.

Answer 1

D.

C.

A,B

Explanation:

Given:

Diameter of a cone-shaped kitchen funnel = 6 inches

Height of a cone-shaped kitchen funnel = 7 inches

Radius of a cylindrical funnel = 4 inches

Height of a cylindrical funnel = 13 inches

To find: Number of cylindrical funnels required to fill a cone-shaped kitchen funnel

Solution:

Radius of a cone-shaped kitchen funnel (R) = 6/2 = 3 inches

Height of a cone-shaped kitchen funnel (H) = 7 inches

Volume of a cone-shaped kitchen funnel =
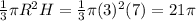`(1)/(3)\pi R^2H=(1)/(3)\pi(3)^2(7)=21\pi` cubic inches

Radius of a cylindrical funnel (r) = 4 inches

Height of a cylindrical funnel (h) = 13 inches

Volume of a cylindrical kitchen funnel =
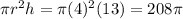`\pi r^2h=\pi(4)^2(13)=208\pi` cubic inches

Number of cylindrical funnels required to fill a cone-shaped kitchen funnel = 9.9≈ 10

Option D. is correct

Given:

Circumference of an orange = 37.68 centimeters

To find: volume of the orange

Solution:

Let r be the radius of the orange

Circumference of an orange = 37.68 centimeters

`2\pi r=37.68\\r=(37.68)/(2\pi)`

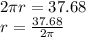
Volume of the sphere =
`(4)/(3)\pi r^3`

`=(4)/(3)\pi \left ( (37.68)/(2\pi) \right )^3`

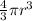
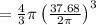
`=(4)/(3)(\left ( 37.68 \right )^3)/(8(3.14)^2)=904.32` cubic metres

Volume of sphere can be computed using only the radius or using only the diameter.

Option A and B are correct.

For volume of cone, both radius and height are required