Question

In a certain school district, it was observed that 32% of the students in the element schools were classified as only children (no siblings). However, in the special program for talented and gifted children, 135 out of 347 students are only children. The school district administrators want to know if the proportion of only children in the special program is significantly different from the proportion for the school district. Test at the α = 0.02 α=0.02 level of significance.

What is the hypothesized population proportion for this test?

Answer 1

We conclude that the proportion of only children in the special program is significantly different from the proportion for the school district.

Explanation:

We are given that in a certain school district, it was observed that 32% of the students in the element schools were classified as only children (no siblings).

However, in the special program for talented and gifted children, 135 out of 347 students are only children.

Let p = population proportion of only children in the special program.

So, Null Hypothesis,
`H_0` : p = 32% {means that the proportion of only children in the special program is equal to the proportion for the school district}

Alternate Hypothesis,
`H_A` : p
`\\eq` 32% {means that the proportion of only children in the special program is significantly different from the proportion for the school district}

The test statistics that would be used here One-sample z proportion statistics;

T.S. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of only children in the special program =
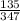`(135)/(347)` = 0.39

n = sample of students = 347

So, test statistics =
`\frac{0.39-0.32}{\sqrt{(0.39(1-0.39))/(347) } }`

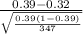
= 2.673

The value of z test statistics is 2.673.

Now, at 0.02 significance level the z table gives critical value of -2.3263 and 2.3263 for two-tailed test. Since our test statistics does not lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the proportion of only children in the special program is significantly different from the proportion for the school district.