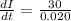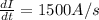Question

LC Circuits: A series circuit contains an 80-μF capacitor, a 0.020-H inductor, and a switch. The resistance of the circuit is negligible. Initially, the switch is open, the capacitor voltage is 50 V, and the current in the inductor is zero. At time t = 0 s, the switch is closed. When the potential across the capacitor is 30 V, what is the rate of change of the current?

Answer 1

The rate of current change in the circuit is
`(dI)/(dt) = 1500 A/s`

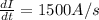
Step-by-step explanation:

From the question we are told that

The capacitor has a value
`C = 80 \mu F`

The inductor has a value
`L = 0.020 H`

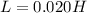
The capacitors voltage is
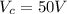`V_c = 50V` at t = 0s

The new capacitor voltage is
`V_c__(n)} = 30 V`

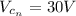
Generally when the switch is closed the potential across the inductor is equal to the potential across the capacitor

So for the inductor

rate of current change is given as

`(dI)/(dt) = (V_l)/(L)`

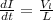
Where
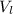`V_l` is the voltage across the inductor.
`V_l = V_c__(n)}`

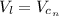
Substituting value

`(dI)/(dt) = (30)/(0.020)`

`(dI)/(dt) = 1500 A/s`