Answer:
We conclude that the proportion of adults who have used a ride‑hailing app is different between college graduates and those without college degrees.
Explanation:
We are given that of the 4787 adults included in the survey, 2369 were college graduates, of which 687 had used a ride‑hailing app.
Among the 2418 adults who had not completed college, 268 has used a ride‑hailing app.
Let
 = proportion of college graduates who have used a ride‑hailing app.
= proportion of college graduates who have used a ride‑hailing app.
 = proportion of without college graduates who have used a ride‑hailing app.
= proportion of without college graduates who have used a ride‑hailing app.
So, Null Hypothesis,
 :
:
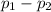 = 0 {means that the proportion of adults who have used a ride‑hailing app is same between college graduates and those without college degrees}
= 0 {means that the proportion of adults who have used a ride‑hailing app is same between college graduates and those without college degrees}
Alternate Hypothesis,
 :
:
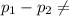 0 {means that the proportion of adults who have used a ride‑hailing app is different between college graduates and those without college degrees}
0 {means that the proportion of adults who have used a ride‑hailing app is different between college graduates and those without college degrees}
The test statistics that would be used here Two-sample z proportion statistics;
T.S. =
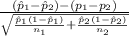 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of college graduates using a ride‑hailing app =
= sample proportion of college graduates using a ride‑hailing app =
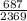 = 0.29
= 0.29
 = sample proportion of without college graduates using a ride‑hailing app =
= sample proportion of without college graduates using a ride‑hailing app =
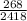 = 0.11
= 0.11
 = sample of college graduates = 2369
= sample of college graduates = 2369
 = sample of without college graduates = 2418
= sample of without college graduates = 2418
So, test statistics =
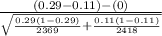
= 15.95
The value of t test statistics is 15.95.
Since, in the question we are not given with the level of significance so we assume it to be 5%. Now, at 5% significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test.
Since, our test statistics does not lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.
Therefore, we conclude that the proportion of adults who have used a ride‑hailing app is different between college graduates and those without college degrees.