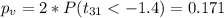Answer:
a)
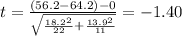
b)
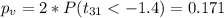
Explanation:
Information given
 represent the mean for sample 1
represent the mean for sample 1
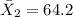 represent the mean for sample 2
represent the mean for sample 2
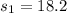 represent the sample standard deviation for 1
represent the sample standard deviation for 1
 represent the sample standard deviation for 2
represent the sample standard deviation for 2
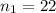 sample size for the group 2
sample size for the group 2
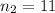 sample size for the group 2
sample size for the group 2
t would represent the statistic (variable of interest)
System of hypothesis
We need to conduct a hypothesis in order to check if the true means are different, the system of hypothesis would be:
Null hypothesis:
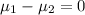
Alternative hypothesis:
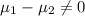
The statistic is given by:
 (1)
(1)
The degrees of freedom are given by:

Part a: Statisitc
Replacing into the formula we got:
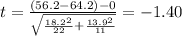
Part b: P value
The p value on this case would be: