Question

A student at a four-year college claims that mean enrollment at four-year colleges is higher than at two-year colleges in the United States. Two surveys are conducted. Of the 35 four-year colleges surveyed, the mean enrollment was 5,135 with a standard deviation of 783. Of the 35 two-year colleges surveyed, the mean enrollment was 4,436 with a standard deviation of 553. Test the student's claim at the 0.01 significance level.

NOTE: If you are using a Student's t-distribution for the problem, including for paired data, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, though.)State the distribution to use for the test. (Enter your answer in the form z or tdf where df is the degrees of freedom. Round your answer to two decimal places.)(1) What is the test statistic? (Round your answer to two decimal places.)(2) What is the p-value? (Round your answer to four decimal places.)

Answer 1

Part 1: The statistic

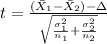`t=\frac{(\bar X_(1)-\bar X_(2))-\Delta}{\sqrt{(\sigma^2_(1))/(n_(1))+(\sigma^2_(2))/(n_(2))}}` (1)

And the degrees of freedom are given by
`df=n_1 +n_2 -2=35+35-2=68`

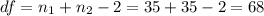
Replacing we got

`t=\frac{(5135-4436)-0}{\sqrt{(783^2)/(35)+(553^2)/(35)}}}=4.31`

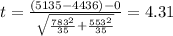
Part 2: P value

Since is a right tailed test the p value would be:

`p_v =P(t_(68)>4.31)=0.000022 \approx 0.00002`

Comparing the p value we see that is lower compared to the significance level of 0.01 so then we can reject the null hypothesis and we can conclude that the mean for the four year college is significantly higher than the mean for the two year college and then the claim makes sense

Explanation:

Data given

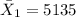`\bar X_(1)=5135` represent the mean for four year college

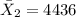`\bar X_(2)=4436` represent the mean for two year college

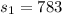`s_(1)=783` represent the sample standard deviation for four year college

`s_(2)=553` represent the sample standard deviation two year college

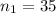`n_(1)=35` sample size for the group four year college

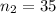`n_(2)=35` sample size for the group two year college

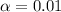`\alpha=0.01` Significance level provided

t would represent the statistic (variable of interest)

System of hypothesis

We need to conduct a hypothesis in order to check if the mean enrollment at four-year colleges is higher than at two-year colleges in the United States , the system of hypothesis would be:

Null hypothesis:
`\mu_(1)-\mu_(2)\leq 0`

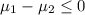
Alternative hypothesis:
`\mu_(1) - \mu_(2)> 0`

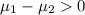
We can assume that the normal distribution is assumed since we have a large sample size for each case n>30. So then the sample mean can be assumed as normally distributed.

Part 1: The statistic

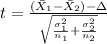`t=\frac{(\bar X_(1)-\bar X_(2))-\Delta}{\sqrt{(\sigma^2_(1))/(n_(1))+(\sigma^2_(2))/(n_(2))}}` (1)

And the degrees of freedom are given by
`df=n_1 +n_2 -2=35+35-2=68`

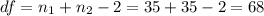
Replacing we got

`t=\frac{(5135-4436)-0}{\sqrt{(783^2)/(35)+(553^2)/(35)}}}=4.31`

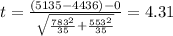
Part 2: P value

Since is a right tailed test the p value would be:

`p_v =P(t_(68)>4.31)=0.000022`

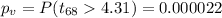
Comparing the p value we see that is lower compared to the significance level of 0.01 so then we can reject the null hypothesis and we can conclude that the mean for the four year college is significantly higher than the mean for the two year college and then the claim makes sense