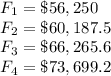Given Information:
Smoothing constant = α = 0.25
Initial forecast salary = F₀ = $55,000
Actual salaries = A = $60,000, $72,000, $84,500, and $96,000
Required Information:
Forecast salaries = F = ?
Answer:
Explanation:
The exponential smoothing model is given by
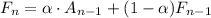
Where
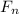 is the forecast salary for nth graduate class
is the forecast salary for nth graduate class
α is the smoothing constant
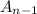 is the actual salary of n - 1 graduate class
is the actual salary of n - 1 graduate class
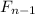 is the forecast salary of n - 1 graduate class
is the forecast salary of n - 1 graduate class
For n = 1
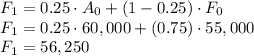
For n = 2
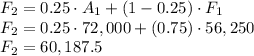
For n = 3
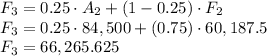
For n = 4
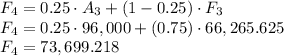
Therefore, the foretasted starting salaries are