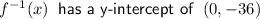Question

Consider the function.

f(x) = -2/3x-24
Which conclusions can be drawn about f^-1(x)? Select two options.

Answer 1

Statement 3

Explanation:

y = -2/3x-24

Make x the subject

y + 24 = -(⅔)x

x = -(3/2)(y + 24)

Intersection variables

f^-1(x) = -(3/2)(x + 24)

Slope: -3/2

No domain restrictions

y-intercept: x = 0

-(3/2)(0+24)

-36

(0,-36)

x-intercepts: y = 0

0 = -(3/2)(x + 24)

x = -24

(-24,0)

Linear function, range is all real values of y

Answer 2

`f^(-1)(x)\: \textsf{ has a y-intercept of }\:(0,-36)`

`f^(-1)(x)\: \textsf{ has a range of all real numbers.}`

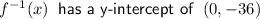
Explanation:

Given function

`f(x)=-(2)/(3)x-24`

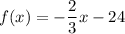
The given function has an unrestricted domain and range.

• Domain: (-∞, ∞) → all real numbers
• Range: (-∞, ∞) → all real numbers

Inverse of a function

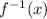`f^(-1)(x)` is the notation for the inverse of the function. The inverse of a function is a reflection in the line y = x

Finding the inverse of the given function

Swap f(x) for y:

`\implies y=-(2)/(3)x-24`

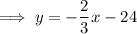
Rearrange the equation to make x the subject:

`\implies -(2)/(3)x=y+24`

`\implies -2x=3y+72`

`\implies x=-(3)/(2)y-36`

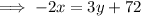
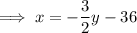
Swap the x for
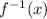`f^(-1)(x)` and the y for x:

`\implies f^(-1)(x)=-(3)/(2)x-36`

The inverse function has a slope of -3/2

The domain of the inverse function is the range of the function.

The range of the inverse function is the domain of the function.

Therefore, the domain and the range are unrestricted.

• Domain: (-∞, ∞) → all real numbers
• Range: (-∞, ∞) → all real numbers

The y-intercept of the inverse function is when x = 0:

`\implies f^(-1)(x)\: \textsf{ has a y-intercept of }\:(0,-36)`

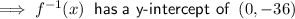
The x-intercept of the inverse function is when y = 0:

`\implies -(3)/(2)x-36=0`

`\implies -(3)/(2)x=36`

`\implies x=-24`

`\implies f^(-1)(x)\: \textsf{ has a x-intercept of }\:(-24,0)`

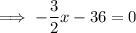
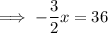
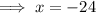
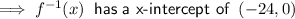
Conclusion

`f^(-1)(x)\: \textsf{ has a y-intercept of }\:(0,-36)`

`f^(-1)(x)\: \textsf{ has a range of all real numbers.}`