Question

The cost function is given by C(x) = 2x 2− 3x + 5, where x is the number of items produced. For what value of x is the AVERAGE cost function minimized?

Answer 1

The average cost is minimized for x=1.58.

Explanation:

The cost function is C(x) = 2x 2− 3x + 5, where x is the number of items produced.

The average cost is C(x)/x, that is the total cost divided by the units produced.

Then the average cost function A(x) becomes:

`A(x)=(C(x))/(x)=(2x^2-3x+5)/(x)=2x-3+5x^(-1)`

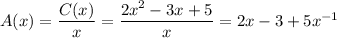
To optimize this function, we derive and equal to zero:

`(dA)/(dx)=0\\\\\\(dA)/(dx)=2+5(-1)x^(-2)=0\\\\\\2-5x^(-2)=0\\\\x^(-2)=2/5\\\\x^2=5/2\\\\x=√(5/2)\approx1.58114\\`

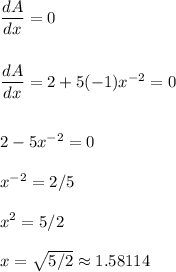
The average cost is minimized for x=1.58.