Question

NEED HELP WITH THESE THREE QUESTIONS!!!

1.) Use the binomial probability formula to find P(x) given that n = 8, p = 0.31, and x = 4.

2.) Suppose that 5 fair coins are tossed all at once. What is the probability that all 5 of them land heads up?

3.)An unprepared student is given a 14 question multiple choice quiz on Reptiles from the Star Wars Saga. Each question has 5 possible answers of which only one is correct. What is the probability that this student answers correctly on less than 4 of these questions?

Answer 1

(a) The value of P (X = 4) is 0.1465.

(b) The probability that all 5 of them land heads up is 0.0313.

(c) The probability that the student answers correctly on less than 4 of these questions is 0.6980.

Explanation:

A Binomial distribution is the probability distribution of the number of successes, X in n independent trials with each trial having an equal probability of success, p.

The probability mass function of a Binomial distribution is:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x);\ x=0,1,2,3...,\ 0<p<1`

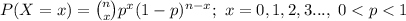
(1)

The information provided is:

X = 4

n = 8

p = 0.31

Compute the value of P (X = 4) as follows:

`P(X=4)={8\choose 4}0.31^(4)(1-0.31)^(8-4)\\=70* 0.00923521* 0.22667121\\=0.146535\\\approx 0.1465`

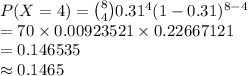
Thus, the value of P (X = 4) is 0.1465.

(2)

The probability of heads, on tossing a single fair coin is, p = 0.50.

It is provided that n = 5 fair coins are tossed together.

Compute the probability that all 5 of them land heads up as follows:

`P(X=5)={5\choose 5}0.50^(5)(1-0.50)^(5-5)\\=1* 0.03125* 1\\=0.03125\\\approx 0.0313`

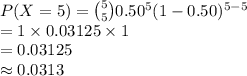
Thus, the probability that all 5 of them land heads up is 0.0313.

(3)

There are 5 possible answers for every multiple choice question. Only one of the five options is correct.

The probability of selecting the correct answer is, p = 0.20.

Number of multiple choice questions, n = 14.

Compute the probability that the student answers correctly on less than 4 of these questions as follows:

P (X < 4) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)

`=\sum\limits^(3)_(x=0){{14\choose x}0.20^(x)(1-0.20)^(14-x)}\\=0.0439+0.1539+0.2501+0.2501\\=0.6980`

Thus, the probability that the student answers correctly on less than 4 of these questions is 0.6980.