Question

A telephone survey of 1000 randomly selected us adults found that 31% of them say they believe in ghosts.14 does this provide evidence that more than 1 in 4 us adults believe in ghosts? clearly show all details of the test. lock, robin h.; lock, patti frazer; morgan, kari lock; lock, eric f.; lock, dennis f.. statistics: unlocking the power of data, 2nd edition (page 418). wiley. kindle edition.

Answer 1

H₀ proportion = 0.25

Hₐ : p ≠ 0.25

z test = 4.38178

Probability = 0.00001177 low, therefore

Yes, more than 0.25 believe in ghosts

Step-by-step explanation:

Here we have

H₀ : p = 0.25

Hₐ : p ≠ 0.25

We derive the test statistic as follows

`z=\frac{\hat{p}-p}{\sqrt{(pq)/(n)}}`

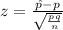
Where:

`\hat p` = Sample proportion = X/n = 31% or 0.31

n = Sample size = 1000

p = Population proportion = 0.25

q = 1 - p

α = 5%

Plugging the values, we have,

`z=\frac{\hat{p}-p}{\sqrt{(pq)/(n)}} = 4.38178`

From which the probability is looked up to be 0.00001177

Whereby as 5% confidence level the critical z = ± 1.96

Therefore, whereby p ≈ 0 <α = 0.05 we reject the null hypothesis, that is there is sufficient statistical evidence that more than 1 in 4 us adults believe in ghost.