Question

Place a number in each box so that each equation is true and each equation has at least one negative number. Choose a number single-digit number starting with the positive number, negative number - not ZERO 2^_x2^_=2^0

Answer 1

x=1, y=-1

Explanation:

Given the equation:
`2^(x)X2^(y)=2^0`

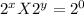
where x and y are the blank boxes.

We want to find

• A positive value of x
• A negative value of y

That makes the equation true.

If x=1, y=-1

`2^(1)X2^(-1)=2^0`

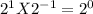
This can be confirmed using addition law of indices(
`a^x+a^y=a^(x+y)`)

`2^(1)X2^(-1)=2^(1+(-1))=2^(1-1)=2^0`

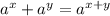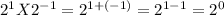
• In general, any pair of a number and its negative value will satisfy the equality.