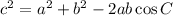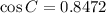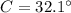Answer:
7. A = 40.8 deg; B = 60.6 deg; C = 78.6 deg
8. A = 20.7 deg; B = 127.2 deg; C = 32.1 deg
Explanation:
Law of Cosines
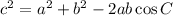
You know the lengths of the sides, so you know a, b, and c. You can use the law of cosines to find C, the measure of angle C.
Then you can use the law of cosines again for each of the other angles. An easier way to solve for angles A and B is, after solving for C with the law of cosines, solve for either A or B with the law of sines and solve for the last angle by the fact that the sum of the measures of the angles of a triangle is 180 deg.
7.
We use the law of cosines to find C.
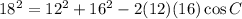
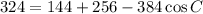
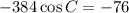
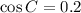
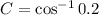
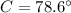
Now we use the law of sines to find angle A.
Law of Sines
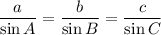
We know c and C. We can solve for a.
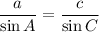
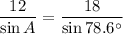
Cross multiply.
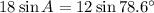
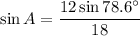
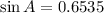
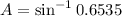
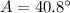
To find B, we use
m<A + m<B + m<C = 180
40.8 + m<B + 78.6 = 180
m<B = 60.6 deg
8.
I'll use the law of cosines 3 times here to solve for all the angles.
Law of Cosines
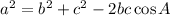
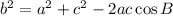
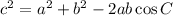
Find angle A:
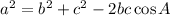

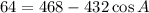
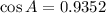
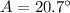
Find angle B:
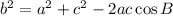
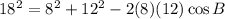

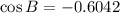
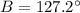
Find angle C: