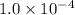Question

Iron (III) oxide and hydrogen react to form iron and water, like this: Fe 03(s)+3H9)2Fe(s)+3HO) At a certain temperature, a chemist finds that a 8.9 L reaction vessel containing a mixture of iron(III) oxide, hydrogen, Iron, and water at equilbrium has the following composition compound amount Fe 3.95 g H 4.77 g Fe 4.38 g H2 2.00 g Calculate the value of the equilibrium constant Kc for this reaction. Round your answer to 2 significant digits.

Answer 1

The question is incomplete, here is the complete question:

Iron (III) oxide and hydrogen react to form iron and water, like this:

`Fe_2O_3(s)+3H_2(g)\rightarrow 2Fe(s)+3H_2O(g)`

At a certain temperature, a chemist finds that a 8.9 L reaction vessel containing a mixture of iron(III) oxide, hydrogen, Iron, and water at equilibrium has the following composition.

Compound Amount

Fe₂O₃ 3.95 g

H₂ 4.77 g

Fe 4.38 g

H₂O 2.00 g

Calculate the value of the equilibrium constant Kc for this reaction. Round your answer to 2 significant digits.

Answer: The value of equilibrium constant for given equation is
`1.0* 10^(-4)`

Step-by-step explanation:

To calculate the molarity of solution, we use the equation:

`\text{Molarity of the solution}=\frac{\text{Mass of solute}}{\text{Molar mass of solute}* \text{Volume of solution (in L)}}`

• For hydrogen gas:

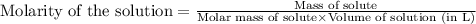
Given mass of hydrogen gas = 4.77 g

Molar mass of hydrogen gas = 2 g/mol

Volume of the solution = 8.9 L

Putting values in above expression, we get:

`\text{Molarity of hydrogen gas}=(4.77)/(2* 8.9)\\\\\text{Molarity of hydrogen gas}=0.268M`

• For water:

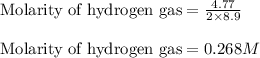
Given mass of water = 2.00 g

Molar mass of water = 18 g/mol

Volume of the solution = 8.9 L

Putting values in above expression, we get:

`\text{Molarity of water}=(2.00)/(18* 8.9)\\\\\text{Molarity of water}=0.0125M`

For the given chemical equation:

`Fe_2O_3(s)+3H_2(g)\rightarrow 2Fe(s)+3H_2O(g)`

The expression of equilibrium constant for above equation follows:

`K_(eq)=([H_2O]^3)/([H_2]^3)`

Concentration of pure solids and pure liquids are taken as 1 in equilibrium constant expression.

Putting values in above expression, we get:

`K_(c)=((0.0125)^3)/((0.268)^3)\\\\K_(c)=1.0* 10^(-4)`

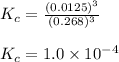
Hence, the value of equilibrium constant for given equation is
`1.0* 10^(-4)`