Question

Two blocks A and B have a weight of 11 lb and 6 lb, respectively. They are resting on the incline for which the coefficients of static friction are μA = 0.15 and μB = 0.26.

Determine the angle θ which will cause motion of one of the blocks.

What is the friction force under each of the blocks when this occurs? The spring has a stiffness of k = 2 lb/ft and is originally unstretched.

Answer 1

the block that starts moving first is block A , fr = 1.625 N , fr = 1.5 N

Step-by-step explanation:

For this exercise we use Newton's second law, for which we take a reference system with the x axis parallel to the plane and the y axis perpendicular to the plane

X axis

fr- Wₓ = 0

fr = Wₓ

Axis y

N-
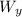`W_(y)` = 0

N = W_{y}

Let's use trigonometry to find the components of the weight

sin θ = Wₓ / W

Cos θ = W_{y} / W

Wₓ = W sin θ

W_{y} = W cos θ

Wₓ = 11 sin θ

W_{y} = 11 cos θ

The equation for friction force is

fr = μ N

We substitute

μ (W cos θ) = W sin θ

μ = tan θ

We can see that the system began to move the angle.

θ = tan⁻¹ μ

So the angles are

Block A θ = tan⁻¹ 0.15

θ = 8.5º

Block B θ = tan⁻¹ 0.26

θ = 14.6º

So the block that starts moving first is block A

The friction force is

Block A

fr = Wx = W sin θ

fr = 11 sin 8.5

fr = 1.625 N

Block B

fr = 6 sin 14.6

fr = 1.5 N