Question

Find the two Z-scores that separate the middle 73.72% on the Standard Normal Curve.

Answer 1

+1.12 and -1.12

Explanation:

Let the two z scores be
`-z_1and+z_1`.

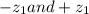Since the two Z-scores that separate the middle 73.72% on the Standard Normal Curve, this can be represented by the equation:

`P(-z_1<Z<z_1)=0.7372\\P(Z<z_1)-P(Z<-z_1)=0.7372\\but P(Z<-z_1)=1-P(Z>-z_1)\\Therefore: P(Z<z_1)-(1-P(Z>-z_1))=0.7372\\P(Z<z_1)-1+P(Z>-z_1)=0.7372\\P(Z<z_1)+P(Z>-z_1)=1+0.7372=1.7372\\P(Z<z_1)+P(Z>-z_1)=1.7372\\but,P(Z<z_1)=P(Z>-z_1)\\Therefore:P(Z<z_1)+P(Z<z_1)=1.7372\\2*P(Z<z_1)=1.7372\\P(Z<z_1)=0.8686`

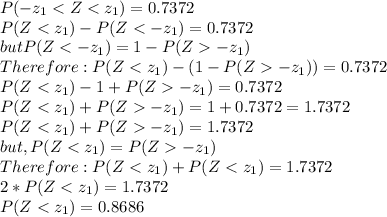
From the z table of the normal distribution, z₁ = 1.12. That is a z score of 1.12 gives 0.8686.

The two z scores are +1.12 and -1.12 = ± 1.12