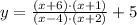Question

Write an equation for a rational function with: Vertical asymptotes at x = 4 and x = -2 x-intercepts at x = -6 and x = -1 Horizontal asymptote at y = 6

Answer 1

`y = ((x+6)\cdot (x+1))/((x-4)\cdot (x+2)) + 5`

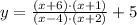
Explanation:

The vertical asymptotes correspond to points where denominator is equalized to zero. Whereas, x-intercepts corresponds to points where numerator is equalized to zero. Lastly, the horizontal asymptote corresponds to the limit of the function when x diverges to plus or minus infinity. Then, the rational equation is:

`y = ((x+6)\cdot (x+1))/((x-4)\cdot (x+2)) + 5`