Question

A simple pendulum and a mass hanging on a spring both have a period of 1 sec when set into oscillatory motion on Earth. They are taken to Planet X, which has the same diameter as Earth but twice the mass. Which is true about the periods of the two objects on Planet X compared to their periods on Earth?

a.Both are shorter.Both are the same.
b.The period of the spring is shorter;
c.the pendulum is the same.
d.The period of the pendulum is shorter;
e.the spring is the same

Answer 1

d.The period of the pendulum is shorter;

e.the spring is the same

The period of a simple pendulum is given by:

`T=2\pi\sqrt{(l)/(g)}`

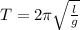
Where l is the pendulum length and g is the gravitational aceleration of the planet.

The period of a mass-spring system is given by:

`T=2\pi\sqrt(m)/(k)`

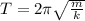
Where k is the spring constant.

The gravitational acceleration on the Earth's surface is defined as:

`g=G(M)/(r^2)`

Here G is the Cavendish constant, M is the Earth mass and r its radius.

For Planet X, we have
`r'=r` and
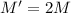`M'=2M`. Thus, the gravity acceleration on this planet is:

`g'=G(M')/(r'^2)\\g'=G(2M)/(r^2)\\g'=2(G(M)/(r^2))\\g'=2g`

Since the period of the pendulum is inversely proportional to gravity, the period of the pendulum is shorter on Planet x. In other hand, the period of the mass-spring system is the same in both planets.