Question

A stock price is currently $50. It is known that at the end of six months it will be either $60 or $42. The risk-free rate of interest with continuous compounding is 12% per annum. Calculate the value (to the nearest cent) of a six-month European call option on the stock with an exercise price of $48. Verify that no-arbitrage arguments and risk-neutral valuation arguments give the same answers. Show your working. Compute the delta of the option as an intermediate step. Compute the probability of an upward stock price movement in a risk-neutral world.as an intermediate step. Assume six months is 0.5 years.

Answer 1

The value of the six-month European call option is 6.96

Calculations:

After 6 months the option value would be either $12 (for stock price of $60) or $0 (for stock price of $42).

Let us consider a portfolio of

+Δ shares

-1: option

The value of this portfolio is either 4Δ or (60Δ - 12) in 6 months.

Now,

if 42Δ = 60Δ - 12,

then,

Δ = 0.6667

The value of the portfolio is 28 (60×0.6667 - 12).

The portfolio is risk-less for this value of Δ.

Current value of the portfolio = 0.6667×50 - f, where f is the value of the option.

As the portfolio must earn the risk-free rate of interest

Thus,

(0.6667×50 - f)
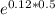`e^(0.12*0.5)`= 28

Or

f = 6.96

Let p be the probability of an upward stock price movement in a risk neutral world.

Therefore,

60*p + 42*(1 - p) = 50*
`e^(0.06)`

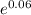
Or

p = 0.616212629

The value option in a risk neutral world is

12*0.6161 + 0*0.3839c = 7.3932

which has a PV of
`7.3932e^(-0.06)`= 6.96