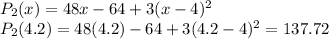Answer:
(a)
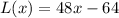
(b)
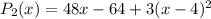
(c)Using Linear Approximation,L(4.2)=137.6
Using Quadratic Approximation,
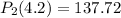
Explanation:
Given:
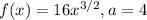
(a)Linear Approximation,
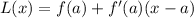
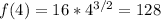
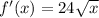
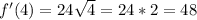
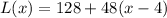
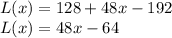
(b)Quadratic Approximation,
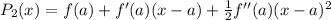
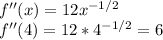
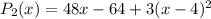
(c)To approximate:
L(x)=48x-64
L(4.2)=48(4.2)-64=137.6
Also, Using Quadratic Approximation