Question

How long does it take to fly from Atlanta to New York’s LaGuardia airport? There are many components of the time elapsed, but one of the more stable measurements is the actual in-air time. For a sample of eighty-three flights between these destinations on Fridays in October, the time in minutes (y) gave the following results:

61 61
Σ yi= 6450 and Σ yi^2=684,900
i=1 i=1

Required:
Find a 99% confidence interval for the average flight time.

Answer 1

The 99% confidence interval for the average flight time is (103.38, 108.10).

Explanation:

The (1 - α)% confidence interval for population mean when the population standard deviation is not known is:

`CI=\bar y\pm t_(\alpha/2, (n-1))* (s)/(√(n))`

The information provided is:

`n=61,\ \ \sum\limits^(61)_(i=1){y_(i)}=6450,\ \ \sum\limits^(61)_(i=1){y_(i)^(2)}=684900`

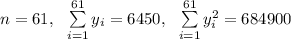
Compute the sample mean as follows:

`\bar y=(1)/(n)\sum\limits^(61)_(i=1){y_(i)}=(6450)/(61)=105.74`

Compute the sample standard deviation as follows:

`s=\sqrt{\frac{n\sum\limits^(61)_(i=1){y_(i)^(2)} - (\sum\limits^(61)_(i=1){y_(i)})^(2)}{n(n-1)}}=\sqrt{(61*684900 - (6450)^(2))/(61(61-1))}=6.9424`

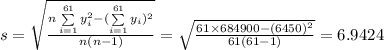
The critical value of t for 99% confidence level and (n - 1) = 60 degrees of freedom is:

`t_(\alpha/2, (n-1))=t_(0.01/2, (61-1))=t_(0.005, 60)=2.66`

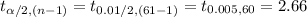
*Use a t-table.

Compute the 99% confidence interval for the average flight time as follows:

`CI=\bar y\pm t_(\alpha/2, (n-1))* (s)/(√(n))`

`=105.74\pm 2.66* (6.9424)/(√(61))\\=105.74\pm 2.3644\\=(103.3756, 108.1044)\\\approx (103.38, 108.10)`

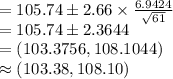
Thus, the 99% confidence interval for the average flight time is (103.38, 108.10).