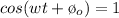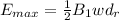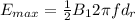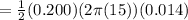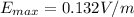Question

Early in 1981 the Francis Bitter National Magnet Laboratory at M.I.T. commenced operation of a 3.3 cm diameter cylindrical magnet, which produces a 30 T field, then the world's largest steady-state field. The field can be varied sinusoidally between the limits of 29.6 and 30.0 T at a frequency of 15 Hz. When this is done, what is the maximum value of the induced electric field at a radial distance of 1.4 cm from the axis

Answer 1

The maximum electric field
`E_(max)= 0.132V/m`

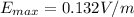
Step-by-step explanation:

From the question we are told that

The diameter is
`d = 3.3 cm = (3.3)/(100) = 0.033m`

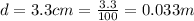
The magnetic field of the cylinder is
`B = 30 T`

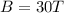
The frequency is
`f = 15Hz`

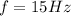
The radial distance is
`d_r = 1.4cm = (1.4)/(100) = 0.014m`

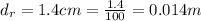
This magnetic field can be represented mathematically as

`B(t) = B_i + B_1sin (wt + \o_i)`

The initial magnetic field is the average between the variation of the magnetic field which is represented as

`B_i = (30 + 29.6)/(2)`

`= 29.8T`

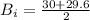
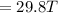
Then
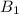`B_1` is the amplitude of the resultant field is mathematically evaluated as

`B_1 = (30.0 - 29.6)/(2)`

`= 0.200T`

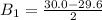
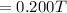
The electric field induced can be represented mathematically as

`E = (1)/(2) [(dB )/(dt) ]d_r`

`= (d_r)/(2) (d)/(dt) (B_i + B_1 sin (wt + \o_o))`

`= (1)/(2) (B wr cos (wt + \o_o))`

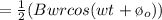
At maximum electric field
`cos (wt + \o_o) = 1`

`E_(max) = (1)/(2) B_1 wd_r`

`E_(max) = (1)/(2) B_1 2 \pi f d_r`

`= (1)/(2) (0.200) (2 \pi (15 ))(0.014)`

`E_(max)= 0.132V/m`