Question

el producto de tres números es 1000 y su suma es 39. Si se sabe que el primero es al segundo como el segundo es al tercero, hallar la diferencia entre el mayor y el menor de los números.

Answer 1

Answer: The difference between the larger and smaller number is 21.

Explanation:

This can be translated to:

"the multiplication between 3 numbers is 1000 and the addition is 39.

If the first number is at the second like the second at the third, find the difference between the smaller and the larger number"

If A is the first number, B the second and C the third we have that:

A*B*C = 1000

A + C + B = 39

A/B = B/C

From the third equation we have that:

A*C = B*B

we can replace it in the first equation and get:

B*(A*C) = 1000

B*B*B = B^3 = 1000

`B = \sqrt[3]{1000} = 10`

So now we have the value of B.

Now we have the two equations:

A + 10 + C = 39

A*C = B*B = 10*10 = 100

We can isolate A in the first equation and get:

A = 39 - 10 - C = 29 - C

now we can replace it in the second equation:

(29 - C)*C = 100

29C - C^2 - 100 = 0

We need to find the roots of that equation, we can use the Bhaskara's function:

`C = (-29 +- √(29^2 - 4*(-1)*(-100)) )/(2*(-1)) = (-29 +- 21)/(-2)`

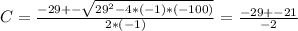
Where we have two possible values for C

C = (-29 - 21)/(-2) = 25

C = (-29 + 21)/(-2) = 4

Let's chose C = 4, because C is the smaller value. (A will take the other value)

Then we have:

A + B + C = 39

A + 10 + 4 = 39

A = 39 - 14 = 25

Then the difference between the larger and smaller number is:

A - C = 25 - 4 = 21