Question

High-strength concrete is supposed to have a compressive strength greater than 6,000 pounds per square inch (psi). A certain type of concrete has a mean compressive strength of 7,000 psi, but due to variability in the mixing process it has a standard deviation of 420 psi, assuming a normal distribution.

What is the probability that a given pour of concrete from this mixture will fail to meet the high-strength criterion?

Answer 1

Probability that a given pour of concrete from this mixture will fail to meet the high-strength criterion is 0.00866.

Explanation:

We are given that High-strength concrete is supposed to have a compressive strength greater than 6,000 pounds per square inch (psi).

A certain type of concrete has a mean compressive strength of 7,000 psi, but due to variability in the mixing process it has a standard deviation of 420 psi, assuming a normal distribution.

Let X = certain type of concrete compressive strength

SO, X ~ Normal(
`\mu=7,000 ,\sigma^(2) =420^(2)`)

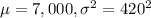The z score probability distribution for normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean compressive strength = 7,000 psi

`\sigma` = standard deviation = 420 psi

SO, Probability that a given pour of concrete from this mixture will fail to meet the high-strength criterion is given by = P(X < 6,000 psi)

P(X < 6,000 psi) = P(
`(X-\mu)/(\sigma)` <
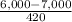`(6,000-7,000)/(420)` ) = P(Z < -2.38) = 1 - P(Z
`\leq` 2.38)

= 1 - 0.99134 = 0.00866

The above probability is calculated by looking at the value of x = 2.38 in the z table which has an area of 0.99134.

Hence, the probability that a given pour of concrete from this mixture will fail to meet the high-strength criterion is 0.00866.