Answer:
The charge of each sphere is
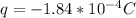
Step-by-step explanation:
The free body diagram of this question is shown on the first uploaded image
From the question we are told that
The mass of the two sphere is
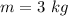
The length of the connection is
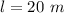
The angle between the suspended side is
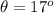
At Equilibrium the force acting at the horizontal is = 0N and the net force acting at the vertical is zero
This can be represented mathematically as
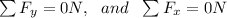
For
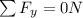
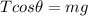
=>
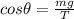
For
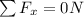
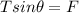
=>

Now

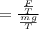
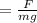
Where F is the electrical force which is mathematically represented as
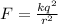
Therefore
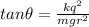
Where
 is the distance between the two masses and from the diagram it is
is the distance between the two masses and from the diagram it is
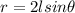
So

making q the subject of the formula
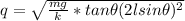
Where k is the Coulomb's constant with a value of
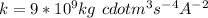
Substituting values

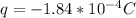
The negative sign is because we are told from the question that they are negatively charged