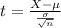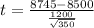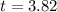Question

The average cost of tuition and room and board at a small private liberal arts college is reported to be $8,500 per term, but a financial administrator believes that the average cost is higher. A study conducted using 350 small liberal arts colleges showed that the average cost per term is $8,745. The population standard deviation is $1,200. Let ? = 0.05. What is the test statistic for this test?A. ±3.82B. +0.204C. -3.82D. +3.82

Answer 1

D. +3.82

Explanation:

The null hypothesis is:

`H_(0) = 8500`

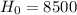
The alternate hypotesis is:

`H_(1) > 8500`

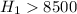
Our test statistic is:

`t = (X - \mu)/((\sigma)/(√(n)))`

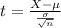
In which X is the sample mean,
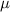`\mu` is the expected mean(null hypothesis),
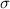`\sigma` is the standard deviation of the population and n is the size of the sample.

In this problem:

`X = 8745, \mu = 8500, \sigma = 1200, n = 350`

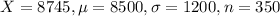
So

`t = (X - \mu)/((\sigma)/(√(n)))`

`t = (8745 - 8500)/((1200)/(√(350)))`

`t = 3.82`