Question

Someeee one?????????????????

Answer 1

Option B)
`a_(n) = 2\cdot 4^(n-1)`

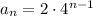
Explanation:

The given geometric sequence is

2, 8, 32, 128,....

The general form of a geometric sequence is given by

`a_(n) = a_(1)\cdot r^(n-1)`

Where n is the nth term that we want to find out.

a₁ is the first term in the geometric sequence that is 2

r is the common ratio and can found by simply dividing any two consecutive numbers in the sequence,

`r=(8)/(2) = 4`

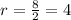
You can try other consecutive numbers too, you will get the same common ratio

`r=(32)/(8) = 4`

`r=(128)/(32) = 4`

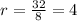
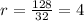
So the common ratio is 4 in this case.

Substitute the value of a₁ and r into the above general equation

`a_(n) = 2\cdot 4^(n-1)`

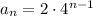
This is the general form of the given geometric sequence.

Therefore, the correct option is B

Note: Don't multiply the first term and common ratio otherwise you wont get correct results.

Verification:

`a_(n) = 2\cdot 4^(n-1)`

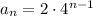
Lets find out the 2nd term

Substitute n = 2

`a_(2) = 2\cdot 4^(2-1) = 2\cdot 4^(1) = 2\cdot 4 = 8`

Lets find out the 3rd term

Substitute n = 3

`a_(3) = 2\cdot 4^(3-1) = 2\cdot 4^(2) = 2\cdot 16 = 32`

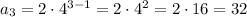
Lets find out the 4th term

Substitute n = 4

`a_(4) = 2\cdot 4^(4-1) = 2\cdot 4^(3) = 2\cdot 64 = 128`

Lets find out the 5th term

Substitute n = 5

`a_(5) = 2\cdot 4^(5-1) = 2\cdot 4^(4) = 2\cdot 256 = 512`

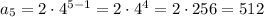
Hence, we are getting correct results!