Question

Alicia has invented a new app that two companies are interested in purchasing for a 2-year contract. Company \text{A}Astart text, A, end text is offering \$10{,}000$10,000dollar sign, 10, comma, 000 for the first month and will increase the amount each following month by \$5000$5000dollar sign, 5000. Company \text{B}Bstart text, B, end text is offering \$500$500dollar sign, 500 for the first month and will double their payment each following month. For which monthly payment will Company \text{B}Bstart text, B, end text's payment first exceed Company \text{A}Astart text, A, end text's payment?

Answer 1

8th month

Explanation:

Answer 2

8th Month

Explanation:

• Company A is offering $10,000 for the first month and will increase the amount each following month by $5000.
• Company B is offering $500 for the first month and will double the amount each following month.

For Company A

Company's A payment increases by a certain amount, it is therefore an Arithmetic Growth.

The nth term for an arithmetic progression is given by:
`U_n=a+(n-1)d`

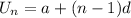
First term, a=$10,000; Common Difference,d=$5000

`\text{Payment for any month n, }U_n=10000+5000(n-1)\\=10000+5000n-5000\\=5000+5000n`

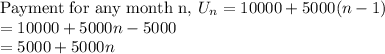
For Company B

Company's B payment doubles every month, it is therefore a Geometric Growth.

The nth term for an geometric progression is given by:
`U_n=ar^(n-1)`

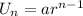
First term, a=$500; Common Ratio,r=2

`\text{Payment for any month n, }U_n=ar^(n-1)=500*2^(n-1)`

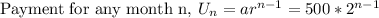
We want to determine at which month, n Company B's Monthly Payment will exceed that of company A.

Using the nth term formula derived above:

`\left|\begin{array}cMonth(n)&B&A\\---&---&---\\1&500&10000\\2&1000&15000\\3&2000&20000\\4&4000&25000\\5&8000&30000\\6&16000&35000\\7&32000&40000\\8&64000&45000\\9&128000&50000\\10&256000&55000\end{array}\right|`

In the 8th Month, the payment of Company B will exceed that of company A.