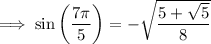Question

Find the value of the function sin 14pi/10

Answer 1

I suppose you mean to find the value of the expression (not function) sin(14π/10).

To start, 14/10 = 7/5.

Next, expand sin(7x) using the angle sum identity,

`\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha`

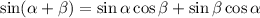
This lets us write

`\sin(7x)=\sin x\cos(6x)+\sin(6x)\cos x`

and we can keep applying the identity to the multiple-angle argument to wind up with

`\sin(7x)=7\cos^6x\sin x-35\cos^4x\sin^3x+21\cos^2x\sin^5x-\sin^7x`

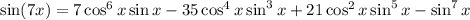
We can replace
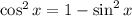`\cos^2x=1-\sin^2x` to write this in terms of sin(x) only.

`\sin(7x)=7\sin x-56\sin^3x+112\sin^5x-64\sin^7x`

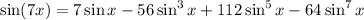
Then we can find the value of sin(7π/5) by plugging in π/5. But to do that, we need to first find the value of sin(π/5).

Using the same process as above, we have

`\sin(5x)=\sin x\cos(4x)+\sin(4x)\cos x=\cdots`

`\sin(5x)=5\cos^4x\sin x-10\cos^2x\sin^3x+\sin^5x`

`\sin(5x)=5\sin x-20\sin^3x+16\sin^5x`

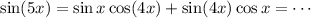
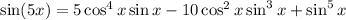
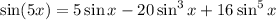
When x = π/5, the left side reduces to sin(π) = 0. Let y = sin(π/5). Then

`0 = 5y-20y^3+16y^5`

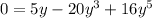
Factorize the right side:

`0=5y(1-4y^2+3y^4)=5y(5-20y^2+16y^4)`

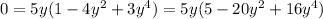
Solving for y tells us that either y = 0 (which can't be true, because 0 < π/5 < π/2 means 0 < sin(π/5) < 1), or

`16y^4-20y^2+5=0`

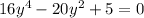
Using the quadratic formula, we find

`y^2=\frac{5\pm\sqrt5}8`

`\implies y=\pm\sqrt{\frac{5\pm\sqrt5}8}`

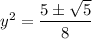
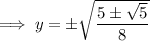
or 4 possible values, approximately -0.5878, 0.5878, -0.9512, or 0.9512.

Of course, only one of these values can be correct. We know sin(π/5) should be positive, so we throw out the two negative options. Also, sin(x) is strictly increasing over (0, π/2). This means 0 < π/5 < π/4 tells us 0 < sin(π/5) < sin(π/4), and sin(π/4) is approximately 0.707. Then sin(π/5) must be 0.5878, or exactly

`\sin\frac\pi5=\sqrt{\frac{5-\sqrt5}8}`

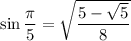
Now plug this into the identity we found for sin(7x).

`\sin\left(\frac{7\pi}5\right)=7\sin\left(\frac\pi5\right)-56\sin^3\left(\frac\pi5\right)+112\sin^5\left(\frac\pi5\right)-64\sin^7\left(\frac\pi5\right)`

`\implies\sin\left(\frac{7\pi}5\right)=-\sqrt{\frac{5+\sqrt5}8}`

Answer 2

The answer is -0.95

Explanation:

I just took the test on edg and got it correct.

follow me on ig- mikaydaeast