Question

Find the equation of the line specified.

The line passes through the points (5,2) and (6,4)

a. y = 2x- 8

b. y = 4x - 8

c. y = 2x + 12

d. y= 2x + 2​

Answer 1

a. y = 2x - 8

General Formulas and Concepts:
Algebra I

Coordinate Plane

• Coordinates (x, y)

Slope Formula:

`\displaystyle m = (y_2 - y_1)/(x_2 - x_1)`

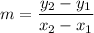
Slope-Intercept Form: y = mx + b

• m - slope
• b - y-intercept

Explanation:

Step 1: Define

Identify given.

Point (5, 2)

Point (6, 4)

Step 2: Find Equation

Finding slope m:

Simply plug in the 2 coordinates into the slope formula to find slope m.

1. [Slope Formula] Substitute in points:
   
   `\displaystyle m = (4 - 2)/(6 - 5)`
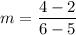
2. Evaluate:
   
   `\displaystyle m = 2`
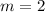
3. [Slope-Intecept Form] Substitute in m:
   
   `\displaystyle y = 2x + b`

∴ our slope m is equal to 2 and our preliminary equation is y = 2x + b.

Finding y-intercept b:

1. [Preliminary Equation] Substitute in point:
   
   `\displaystyle 2 = 2(5) + b`
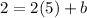
2. Simplify:
   
   `\displaystyle 2 = 10 + b`
3. Solve:
   
   `\displaystyle b = -8`

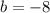
∴ the y-intercept b is equal to -8.

Finding line equation:

1. [Slope-Intercept Form/Preliminary Equation] Substitute in b:
   
   `\displaystyle y = 2x - 8`

∴ the equation of the line is equal to y = 2x - 8.

---

Topic: Algebra I