Question

A transverse wave produced near one end of an extremely long vibrating string is described by the equation below. (Ignore wave reflections from the other end of the string, which is extremely far ahead.) The linear density of this string is 0.0073 kg/m. What must be the tension applied to this string?Between 350 N and 400 N.

Between 250 N and 300 N.
Between 400 N and 450 N.
Between 150 N and 200 N.
Between 300 N and 350 N.
Between 100 N and 150 N.
Between 200 N and 250 N.

Answer 1

between 450N and 500N

Step-by-step explanation:

The complete question is:

A transverse wave produced near one end of an extremely long vibrating string is described by the equation below. (Ignore wave reflections from the other end of the string, which is extremely far ahead.) The linear density of this string is 0.0073 kg/m. What must be the tension applied to this string?

y(x,t)=.0321m * sin (2.05x-524t + pi/4)

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

To find the tension in the string you use the formula for the speed of the wave in a string:

`v=\sqrt{(T)/(\mu)}`

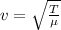
T: tension

mu: linear density of the string = 0.0073kg/m

Then, it is necessary to calculate v. This is made by using information from the wave equation:

`y(x,t)=Asin(kx-\omega t+\phi)\\\\k=2.05m^(-1)\\\\\omega=524s^(-1)\\\\v=(\omega)/(k)=(524)/(2.05)(m)/(s)=255.6(m)/(s)`

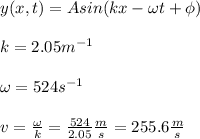
by replacing the value of v in (1), and doing T the subject of the formula you obtain:

`T=v^2\mu=(255.05m/s)^2(0.0073kg/m)=476.95N`

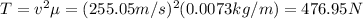
hence, the tension applied is between 450N and 500N