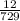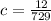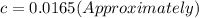Question

Two streams flow into a reservoir. Let X and Y be two continuous random variables representing the flow of each stream with joint pdf: f(x, y) = cx y(1 + y) for 0 ≤ x ≤ 3 and 0 ≤ y ≤ 3, f(x, y) = 0 otherwise. The value c, a constant, is approximately equal to:

Answer 1

c = 0.165

Explanation:

Given:

f(x, y) = cx y(1 + y) for 0 ≤ x ≤ 3 and 0 ≤ y ≤ 3,

f(x, y) = 0 otherwise.

Required:

The value of c

To find the value of c, we make use of the property of a joint probability distribution function which states that

`\int\limits^a_b \int\limits^a_b {f(x,y)} \, dy \, dx = 1`

where a and b represent -infinity to +infinity (in other words, the bound of the distribution)

By substituting cx y(1 + y) for f(x, y) and replacing a and b with their respective values, we have

`\int\limits^3_0 \int\limits^3_0 {cxy(1+y)} \, dy \, dx = 1`

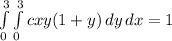
Since c is a constant, we can bring it out of the integral sign; to give us

`c\int\limits^3_0 \int\limits^3_0 {xy(1+y)} \, dy \, dx = 1`

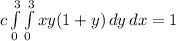
Open the bracket

`c\int\limits^3_0 \int\limits^3_0 {xy+xy^(2) } \, dy \, dx = 1`

Integrate with respect to y

`c\int\limits^3_0 {(xy^(2))/(2) +(xy^(3))/(3) } \, dx (0,3}) = 1`

Substitute 0 and 3 for y

`c\int\limits^3_0 {((x* 3^(2))/(2) +(x * 3^(3))/(3) ) - ((x* 0^(2))/(2) +(x * 0^(3))/(3))} \, dx = 1`

`c\int\limits^3_0 {((x* 9)/(2) +(x * 27)/(3) ) - (0 +0) \, dx = 1`

`c\int\limits^3_0 {((9x)/(2) +(27x)/(3) ) \, dx = 1`

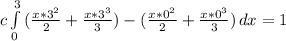
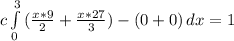
Add fraction

`c\int\limits^3_0 {((27x + 54x)/(6)) \, dx = 1`

`c\int\limits^3_0 {(81x)/(6) \, dx = 1`

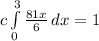
Rewrite;

`c\int\limits^3_0 (81x * (1)/(6)) \, dx = 1`

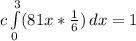
The
`(1)/(6)` is a constant, so it can be removed from the integral sign to give

`c * (1)/(6)\int\limits^3_0 (81x ) \, dx = 1`

`(c)/(6)\int\limits^3_0 (81x ) \, dx = 1`

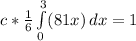
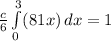
Integrate with respect to x

`(c)/(6) * (81x^(2))/(2) (0,3) = 1`

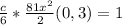
Substitute 0 and 3 for x

`(c)/(6) * (81 * 3^(2) - 81 * 0^(2))/(2) = 1`

`(c)/(6) * (81 * 9 - 0)/(2) = 1`

`(c)/(6) * (729)/(2) = 1`

`(729c)/(12) = 1`

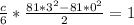
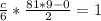
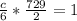
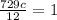
Multiply both sides by
`(12)/(729)`

`c = (12)/(729)`

`c = 0.0165 (Approximately)`