Answer:
It takes 2.24 s for the phone to land.
Explanation:
The height of the phone as it drops can be modeled with the equation
h= -16t²+80
where h is measured in feet and t represents the number of seconds since the phone was dropped.
When the phone hits the ground then height of the phone becomes zero.
i.e h=0
-16t²+80=0
⇒16t²=80
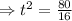
⇒ t² =5
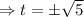
∴t=2.24 s [ since time can not negative]
It takes 2.24 s for the phone to land.