Question

The height of a trapezoid is 8 in. And its area is 96 in2. One base of the trapezoid is 6 inches longer than the other base. What are the lengths of the bases? Complete the explanation of how you found your answer. One base is Use the formula for the area of a trapezoid. Substitute 96 for A and 8 for h and simplify the equation to find = (b1 + b2). Use guess and check to find two numbers that add to with one number 6 more than the other to get

Answer 1

The lengths of the bases are 9 inches and 15 inches.

Explanation:

The area of trapezoid is

`=\frac12(\textrm{ sum of parallel sides})* height`

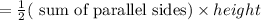
Given that the height of a trapezoid is 8 in. and its area is 96 in².

Assume the bases of the trapezoid be b₁ and b₂.

Since one base of the trapezoid 6 in. longer than the other.

Let, b₁=b₂+6

The area of the trapezoid is

`=\frac 12 (b_1+b_2)*8` in²

`=\frac12 (b_2+6+b_2)* 8` in²

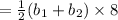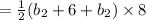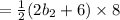`=\frac12(2b_2+6)*8` in²

According to the problem,

`\frac12(2b_2+6)*8 =96`

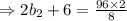`\Rightarrow 2b_2+6=(96* 2)/(8)` [ Multiplying
`\frac28` ]

`\Rightarrow 2b_2+6=24`

`\Rightarrow 2b_2=24-6`

`\Rightarrow 2b_2=18`

`\Rightarrow b_2=(18)/(2)`

`\Rightarrow b_2=9`

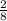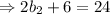
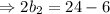
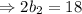
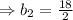
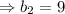
Then,
`b_1=b_2+6`

=9+6

=15 in

The lengths of the bases are 9 inches and 15 inches.