Question

A 95 percent confidence interval for the mean of a population is to be constructedand must be accurate within 0.3 unit. A preliminary sample standard deviation is2.9. The smallest sample size n that provides the desired accuracy with 95 percentconfidence is:________.A. 400 B. 359 C. 389 D. 253

Answer 1

B. 359

Explanation:

Given that:

The margin of error (e) must be within 0.3 unit, The standard deviation (σ) = 2.9 and the the confidence level = 95% = 0.95

α = 1 =0.95 = 0.05

`(\alpha)/(2)=(0.05)/(2)=0.025`

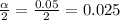
The z score of 0.025 corresponds to the z score of 0.0475 (0.5 - 0.025) which can be gotten from the normal probability table.

Therefore:
`z_(\alpha)/(2)= z_(0.025)=1.96`

The formula for the margin of error is given by:

`e=z_(0.025)(\sigma)/(√(n) ) \\Substituting:\\0.3=1.96*(2.9)/(√(n) ) \\√(n)=(1.96*2.9)/(0.3)\\√(n) =18.95\\ n=18.95^2=359`

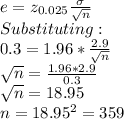
Therefore the smallest sample size (n) is 359