Answer:
|a-b|=6.34m
Step-by-step explanation:
To find the difference between the vector you can use the formulas for the magnitude of a vector and also for the doc product between two vectors:
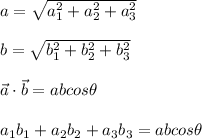
a1, a2, a3: components of a vector
b1, b2, b3: components of b vector
a: magnitude of a = 2m
b: magnitude of b = 8m
angle = 30°
By squaring the first two equations
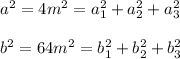
Then, you multiply by 2 the third equation:
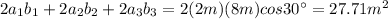
Now, you sum the first two equations ans take the difference with the third equation. Thus, you obtain a perfect square trinomial:
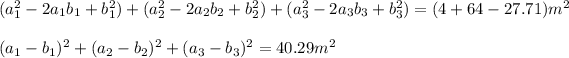
This last expression is the square of the magnitude of the difference a-b. Hence you have:
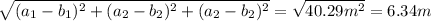
thus, the magnitude of the difference is 6.34m