Question

Two balls of mass 0.09 kg hang on strings attached to the same point on the ceiling. The balls are given charges Q that cause them to repel. Once in equilibrium, the strings make 45-degree angles with the vertical, and the spheres are separated by 2 meters. The charge Q on each sphere is:________.

Answer 1

Q = 6.33μC

Step-by-step explanation:

To find the value of the charge Q you take into account both gravitational force and electric force over each ball. By symmetry you can use the fact that both balls experiences the same forces. Hence you only take into account the forces for one ball for the x component and y component:

`-Mg+Tcos\theta=0\\\\F_e-Tsin\theta=0`

M: mass of the ball = 0.09kg

T: tension of the string

F_e: electric force between charges

angle = 45°

The electric force is given by:

`F_e=k(Q^2)/(r^2)`

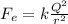
Q: charge of the balls

r: distance between balls = 2m

You divide both equation in order to eliminate the tension T:

`tan\theta=(F_e)/(Mg)=k(Q^2)/(Mgr^2)`

By doing Q the subject of the formula and replacing you obtain:

`Q=\sqrt{(tan\theta Mgr^2)/(k)}=\sqrt{(tan45\°(0.09kg)(2m)^2)/((8.89*10^(9)Nm^2/C^2))}=6.33*10^(-6)C=6.33\mu C`

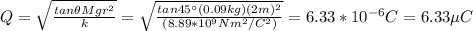
hence, the charge of the balls is 6.33μC