Question

A 8.48-kg box is sliding across the horizontal floor of an elevator. The coefficient of kinetic friction between the box and the floor is 0.415. Determine the kinetic frictional force that acts on the box when the elevator is (a) stationary, (b) accelerating upward with an acceleration whose magnitude is 1.91 m/s2, and (c) accelerating downward with an acceleration whose magnitude is 1.91 m/s2.

Answer 1

(a) 34.48N

(b) 27.7664N

(c)41.209N
`a = 7.89m/s^2`

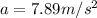
Step-by-step explanation:

Following relation gives force of kinetic friction.

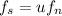`f_(s) =uf_(n)` , u is coefficient of of kinetic friction ,
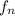`f_n` is force normal or perpendicular to surface which is given by
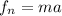`f_n = ma`, a is acceleration normal to surface.

In case of b and c, a is varied because of the acceleration of elevator and in case a it remains
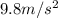`9.8m/s^2` because elevator is stationary and acceleration is only due to earth's gravity.

so in case b
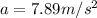`a = 7.89m/s^2` and in case c
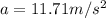`a = 11.71m/s^2` (it is net acceleration ).

substituting all this in original relation gives.

(a)
`f_s=0.415*8.48kg*9.8m/s^2=34.48N.`

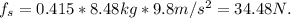
(b)
`f_s = 0.415*8.48kg*7.89m/s^2=27.7664N`.

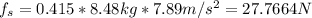(c)
`f_s=0.415*8.48kg*11.71m/s^2=41.209N`.