Answer:
6.6 m/s
Step-by-step explanation:
We are given that
Length,l=14 m
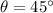
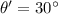
We have to find the Tarzan's speed before he reaches Jane.
Difference in height,h=Final height-Initial height=l(cos 30-cos 45)
Substitute the values
h=14(cos30-cos45)=2.22 m
Speed of Tarzan is given by
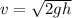
Where

Substitute the values
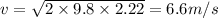
Hence, Tarzan's speed just before he reaches Jane=6.6 m/s