Answer:
a) 40 different hamburgers can be ordered with exactly three extras
b) 20 different regular hamburgers can be ordered with exactly three extras
c) 7 different regular hamburgers can be ordered with at least five extras
Explanation:
The order in which the extras are ordered is not important. So we use the combinations formula to solve this question.
Combinations formula:
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

In this problem:
2 options of hamburger(regular or larger)
6 options of extras(cheese, relish, lettuce, tomato, mustard, or catsup.).
(a) How many different hamburgers can be ordered with exactly three extras?
1 hamburger type, from a set of 2.
3 extras, from a set of 6. So
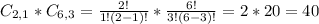
40 different hamburgers can be ordered with exactly three extras
(b) How many different regular hamburgers can be ordered with exactly three extras?
3 extras, from a set of 6. So
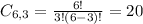
20 different regular hamburgers can be ordered with exactly three extras
(c) How many different regular hamburgers can be ordered with at least five extras?
Five extras:
5 extras, from a set of 6. So
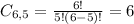
Six extras:
6 extras, from a set of 6. So

6 + 1 = 7
7 different regular hamburgers can be ordered with at least five extras