Question

What is the equation of the line that passes through the point (-3, 4) and has a slope of 1?

Answer 1

`y=x+7`

Explanation:

We can use the equation y=mx+b to solve this problem.

First, we know the 'm' or slope of the line, so we'll substitute that into the equation.

`y=mx+b\\y=1x+b\\y=x+b`

Now, let's solve for b. We already have x and y values - x= -3 and y=4. Let's substitute that into y=x+b and solve.

`y=x+b\\4=-3+b\\b=4+3\\b=7`

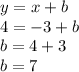
Finally, let's plug the slope and y intercept ('b') back into y=mx+b.

`y=mx+b\\y=(1)x+(7)\\y=x+7`

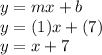
That's the answer to this problem.

I hope this helps.