Answer:
0.0007872
Explanation:
-Since the sample size is large enough, we apply the normal distribution to find the probability.
#Given n=96, mean=38 and standard deviation=6.2 pounds, the probability can be calculated as:
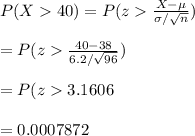
Hence, the probability is 0.0007872