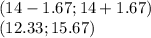Question

How much money does the average professional hockey fan spend on food at a single hockey​ game? That question was posed to 10 randomly selected hockey fans. The sampled results show that sample mean and standard deviation were $ 14 and $ 2.70, respectively. Use this information to create a 95% confidence interval for the mean. Express the answer in the form

Answer 1

The confidence interval is

`(12.33 ; 15.67)`

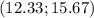
Explanation:

Givens

• The sample mean is 14.
• The standard deviation is 2.70.
• The confidence interval is 95%.

To find a confidence interval we have to use the formula

`\mu (+-)z* (\sigma)/(√(n) )`

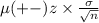
Where
`\mu` is the mean,
`z` is the z-value for a 95% confidence level,
`\sigma` is the standard deviation and
`n` is the sample size.

The z-value for 95% confidence is 1.96.

Replacing all values, we have

`14(+-)1.96* (2.70)/(√(10) )=14(+-)1.96 * (2.70)/(3.16)=14(+-)1.67`

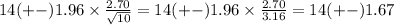
Which means the confidence interval is

`(14-1.67 ;14+1.67)\\(12.33 ; 15.67)`